A Gentle Tutorial on Linear Algebra with Python

Published on Thursday, 21-08-2025

#Tutorials

(Adopted from CS221)

image info

πŸ”’ A Gentle Tutorial on Linear Algebra with Python

Linear Algebra is the foundation of modern data science, computer graphics, and machine learning. In this tutorial, we’ll walk through key concepts step by stepβ€”using notation, Python code, and visualizations to make things clear.

1. Vectors

A vector is an ordered list of numbers. It can represent quantities like position, velocity, or weights in a neural network.

Notation:

v=[v1v2v3]\mathbf{v} = \begin{bmatrix} v_1 \\ v_2 \\ v_3 \end{bmatrix}

Example:

v=[23]\mathbf{v} = \begin{bmatrix} 2 \\ 3 \end{bmatrix}

Python:

import numpy as np

# define a vector
v = np.array([2, 3])
print("Vector v:", v)

2. Vector Norm

The norm measures the β€œlength” or β€œmagnitude” of a vector. For vector v=[v1,v2,…,vn]\mathbf{v} = [v_1, v_2, \dots, v_n]:

βˆ₯vβˆ₯2=v12+v22+β‹―+vn2\| \mathbf{v} \|_2 = \sqrt{v_1^2 + v_2^2 + \dots + v_n^2}

This is the Euclidean norm (L2 norm).

Python:

norm_v = np.linalg.norm(v)
print("Norm of v:", norm_v)

3. Vector Normalization

To normalize a vector, divide it by its norm so its length becomes 1:

v^=vβˆ₯vβˆ₯\hat{\mathbf{v}} = \frac{\mathbf{v}}{\|\mathbf{v}\|}

Python:

v_normalized = v / np.linalg.norm(v)
print("Normalized v:", v_normalized)

4. Vector Operations

  • Addition:
u+v=[u1+v1,u2+v2,… ]\mathbf{u} + \mathbf{v} = [u_1+v_1, u_2+v_2, \dots]
  • Scalar Multiplication:
cv=[cv1,cv2,… ]c \mathbf{v} = [c v_1, c v_2, \dots]

Python:

u = np.array([1, 4])
add = u + v
scalar_mul = 3 * v
print("u + v =", add)
print("3 * v =", scalar_mul)

5. Dot Product

The dot product measures similarity between two vectors:

uβ‹…v=βˆ‘i=1nuivi\mathbf{u} \cdot \mathbf{v} = \sum_{i=1}^{n} u_i v_i

It’s also related to the angle ΞΈ\theta between vectors:

uβ‹…v=βˆ₯uβˆ₯βˆ₯vβˆ₯cos⁑(ΞΈ)\mathbf{u} \cdot \mathbf{v} = \|\mathbf{u}\|\|\mathbf{v}\|\cos(\theta)

Python:

dot = np.dot(u, v)
print("u Β· v =", dot)

6. Matrices

A matrix is a 2D array of numbers:

A=[123456]A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix}

Python:

A = np.array([[1, 2, 3],
              [4, 5, 6]])
print("Matrix A:\n", A)

7. Matrix-Vector Multiplication

If AA is a matrix of size mΓ—nm \times n and x\mathbf{x} a vector of size nn:

Ax=y,y∈RmA \mathbf{x} = \mathbf{y}, \quad \mathbf{y} \in \mathbb{R}^m

Example:

[123456][10βˆ’1]=[βˆ’2βˆ’2]\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} \begin{bmatrix} 1 \\ 0 \\ -1 \end{bmatrix} = \begin{bmatrix} -2 \\ -2 \end{bmatrix}

Python:

x = np.array([1, 0, -1])
y = A @ x
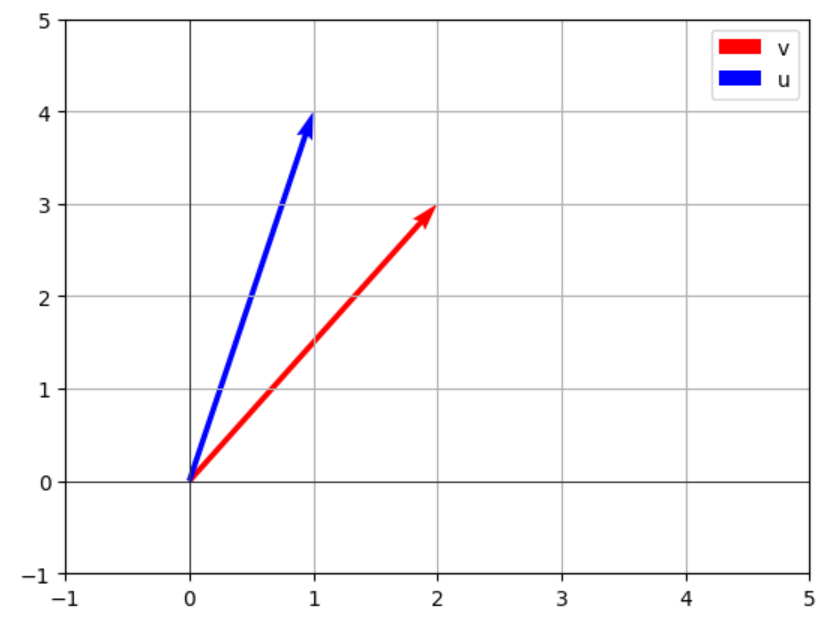
print("A * x =", y)

8. Visualizing Vectors

We can visualize 2D vectors using matplotlib:

import matplotlib.pyplot as plt

# plot vectors
origin = [0], [0]  # starting point
plt.quiver(*origin, v[0], v[1], angles='xy', scale_units='xy', scale=1, color='r', label="v")
plt.quiver(*origin, u[0], u[1], angles='xy', scale_units='xy', scale=1, color='b', label="u")

plt.xlim(-1, 5)
plt.ylim(-1, 5)
plt.axhline(0, color='black', linewidth=0.5)
plt.axvline(0, color='black', linewidth=0.5)
plt.grid()
plt.legend()
plt.show()

This will plot u (blue) and v (red) from the origin.

βœ… Conclusion

In this tutorial, we covered:

  • What vectors are, their norms, and normalization
  • Vector operations (addition, scaling, dot product)
  • Matrices and matrix-vector multiplication
  • Visualizing vectors in 2D

These foundations are essential for deeper topics like linear transformations, eigenvalues, and machine learning applications.